Hour of Code

Today in Geometry, we learned how important code is, and how we use it everyday. We chose the Frozen characters, and we moved them with different equations of code. One thing I found difficult, was figuring out how many degrees to make each turn. I learned how to place each code into a certain order to make the character move how I want them to. I also enjoyed how the codes got more difficult as you completed each level. Here is one of the codes I put together.

for (var count = 0; count < 90; count++) {
  penColour(colour_random());
  moveForward(100);
  moveBackward(100);
  turnRight(4);
}

GeomeTREE (Two Intersecting Tetrahedra)

A polyhedron is a solid figure with many plane faces, typically more than six.A polygon has 3 sides or more and a polyhedron has 6 sides or more. A polyhedron has twice as many sides as a polygon. My ornament was a Stellated Octangula (Two Intersecting Tetrahedra.) It consists of two pyramids formed by connecting 8 triangles. I used blue and pink construction paper to form my ornament. I connected the vertices with tape and glue. All of the sides intersected by the way that they were formed. None of the planes on my ornament were parallel, but the segments formed two large pyramids.

Reflection- I worked by myself on this project It took me roughly about two class periods. I learned about Stellated Octangulas. In the word "Octangula," the word "octa" means 8. I used 8 triangles to form this ornament. The word "Tetrahedra," has the word "tetra," which means 4. Two intersecting- would stand for the two pyramids built into the ornament itself. The most challenging part was getting the triangles to stick together with the tape and the glue. I liked how the project was to make ornaments for the Christmas tree. The only thing fixable, was maybe an easier way to get the triangles to stick together to form the ornament. 

Polygons

Polygon- plane shape (two dimensional) with straight sides

Triangle- 3 sides

Quadrilateral- 4 sides

Pentagon- 5 sides

Hexagon- 6 sides 

Heptagon- 7 sides

 









Octagon- 8 sides

So Far

3 Things I have Learned this Year~

1- I have learned how to use a compass to show different answers for different equations
2- I have learned how to label different triangles
3- I have learned that the long side of the triangle is called the hypotenuse

My Favorite Thing in Math So Far~ Being able to solve different equations with different methods to guide me towards the answer.

To Make This Class Better~ I would like to use the white boards more and possibly have more time to work on notes and homework.

Something I am Proud of This Year~ I am proud that I learned how to make a descriptive note sheet for each lesson we have learned so far.

Converse

Converse Statement~ The converse of an if-then statement is the statement formed by switching the hypothesis and the conclusion. It can be true or false.

True Converse Statement~ If you see the ocean, then you are at the beach. If you are at the beach, then you see the ocean.

False Converse Statement~ If you are eating ice-cream, then you are at Chickfila. If you are at Chickfila, then you are eating ice-cream.

Parallel vs. Non-Parallel

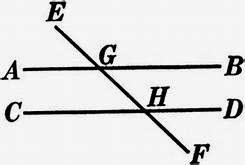
 A Line Crosses A Pair of Parallel Lines

 

    If a set of 2 parallel lines, line l and line m, are crossed or cut by another line, line n, we say "a set of parallel lines are cut by a transversal."

    Each of the parallel lines cut by the transversal has 4 angles surrounding the intersection.

 

    These are matched in measure and position with a counterpart at the other parallel line.

 

    At each of the parallel lines, there are two pairs of vertical angles. Each angle in the pair is congruent to the other angle in the pair.

 

 1  4, angle 1 is congruent to angle 4.

 2  3, angle 2 is congruent to angle 3.

 

 5  8, angle 5 is congruent to angle 8.

 6  7, angle 6 is congruent to angle 7.

                                                 Parallel Lines Cut by a Transversal 

Non-Parallel Lines Cut by a Transversal

Transversal

A line that cuts across a set of lines or the side of a plane figure. Transversals often cut across parallel lines.

Properties of Transversals

                                                       Two Lines Cut by a Transversal

Transversal~ is a line that intersects two or more coplanar lines at different points
Corresponding Angles~ two angles that occupy corresponding positions
Alternate Interior Angles~ two angles that lie between the two lines on the opposite sides of the transversal
Alternate Exterior Angles~ two angles that lie outside the two lines on the opposite sides of the transversal
Same-Side Interior Angles~ two angles that lie between the two lines on the same side of the transversal

Advertising Project

Inductive Reasoning is reasoning in which the premises seek to apply strong evidence for the truth of the conclusion. Deductive Reasoning is reasoning the process of reasoning from one or more statements to reach a logically certain conclusion.


https://www.youtube.com/watch?v=fG3_kC5Gxv0

Overview~ In this clip, they are using inductive reasoning to prove to the viewers that faster is better. They use little kids in this advertisement to show that faster is better in all different situations. 

If faster is better, then slower is worse. 

Reason for Reason- Inductive reasoning seeks to apply strong evidence for the subject being proven. The people who make advertisements every day, seek for people to remember their clips, and buy their products. 

Personal Relation~ This relates to us everyday, because we are a generation of inductive reasoning. We might have a question in class, and give proof to back up our statement. We also might want to campaign for something, and to get people to vote for us, we show them with proof how we can be a great leader.

Chalk Lines

     <1 Equals 90º and <2 Equals 90º so <1 is congruent to <2

      <1 and <2 are supplementary angles and are equal to each other 

Non Parallel Lines vs. Skew Lines

Non Parallel Lines- Slanting or inclined in direction or course or position--neither parallel nor perpendicular nor right-angled.

Skew Lines- Two straight lines that do not lie in the same plane, are not parallel, and do not intersect, the distance between them being the unique segment perpendicular to both lines.

Perpendicular and Parallel Lines

Parallel Lines- Two lines that lie on the same plane and do not intersect.

Perpendicular Lines- Two lines that intersect to form a right angle.

Stew Lines- Two lines that do not lie on the same plane and do not intersect.

Linear Pair and Vertical Angles

Linear Pair~ A linear pair is a pair of adjacent, supplementary angles. Adjacent means next to each other and supplementary means that the measures of the two angles add up to equal 180 degree.

Vertical Angles~ Each of the pairs of opposite angles made by two intersecting lines.

Syllogism

If it is fall, then Christmas is around the corner.
+
If Christmas is around the corner, then I am excited.
=
If it is  fall, then I am excited.




Syllogism~  logical argument that applies deductive reasoning to arrive at a conclusion based on two or more propositions that are asserted or assumed to be true.

The Difference Between Complementary and Supplementary Angles

Complementary Angles~ Two angles are Complementary Angles if the sum of their measures is 90 degrees. Supplementary Angles~ Two angles are Supplemetary Angles if the sum of their measures is 180 degrees. The difference between the two types of angles, is that Complementary Angles add up to be 90 degrees, and Supplementary Angles add up to be 180 degrees.

Desmos Geo House

 On my graph, I used an actuate angle, obtuse angle, a line segment, and a few right angles. On (9,0 and 9,-4) I had an acute angle. On (9,18 and -10,18) I had an obtuse angle. On (-9,-8 and 9,-8) I have my two right angles. And lastly on (-8) I have my line segment. My biggest challenge was trying to get my obtuse and acute angles into my graph. I have learned how to incorporate these kinds of angles into my future graphs.

How many Handshakes?

The Handshake Function Rule would be f(n)= n(n-1)/2. Ex. 1 person... 1(1-1)/2=0    Ex.3 people... 3(3-1)/2=3. The process to find out how many handshakes you can make with a certain number of people is simple if you plug it into the formula. Another way to find out how many handshakes you can make with a certain number of people can be sketched... Ex. 1 person... {  .  }= 0 handshakes. 2 people...{  .-.  }= 1 handshake. My final conclusion is that there are many ways to find out how many handshakes can be made between a certain number of people.

Why Math?

I think that the three different doorways of math are personal, practical, and spiritual. On a personal level, you can relate Math and creativity to things that are happening in your own life. On a practical level, you have to learn math, because it is the foundation for everything you do in college, and in your job in the future. On a spiritual level, you learn math to see the creativity that God has given to us in our life. You can see these three concepts through Math, and the way that we breakdown every problem. Right now, the one that stands out to me the most is the practical concept of math, because right now in my life, you really need to comprehend the idea of Math to help mold your base for the rest of your school career. In Genesis 1:1, God talks about creating the Heavens and the Earth. This shows how God had a mold of the universe before he started to work on it. You have to have a firm foundation spiritually and mentally to accomplish these things.

Hello World!

Hi, I'm Payton. Right now the four most important things to me are family, friends,school, and competition cheerleading. This year I am excited about being in High School, and learning new concepts in all of my classes. I'm defiantly anxious about exams this year. One thing you may not know about me is that my family loves to travel to the Caribbean.